运算方法和运算电路

基本运算部件

---

全加器(Full-Adder, FA)

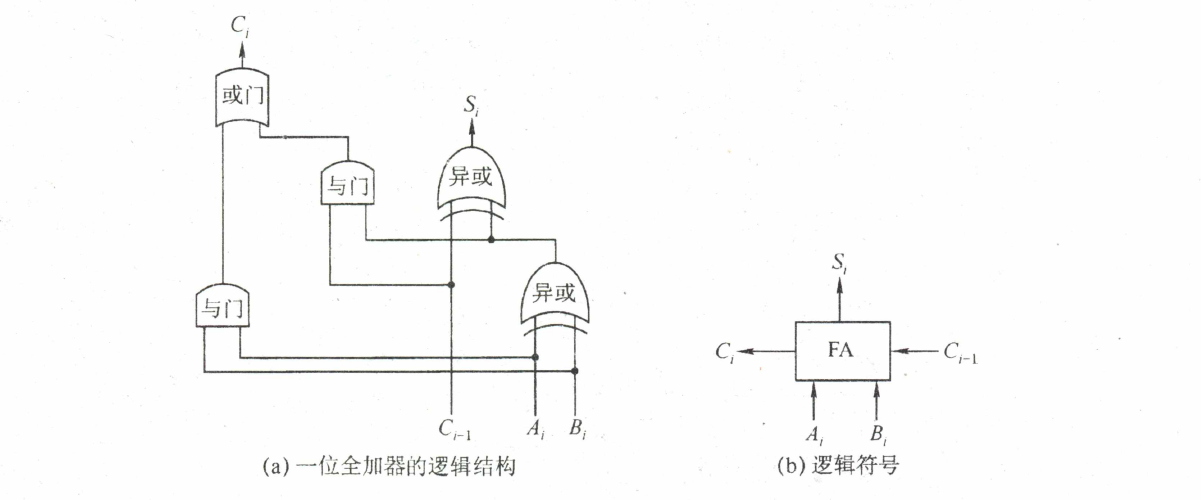
$$
S_{i} = A_{i} \oplus B_{i} \oplus C_{i - 1} \ \
C_{i} = A_{i}B_{i} + (A_{i} \oplus B_{i}) C_{i - 1}
$$

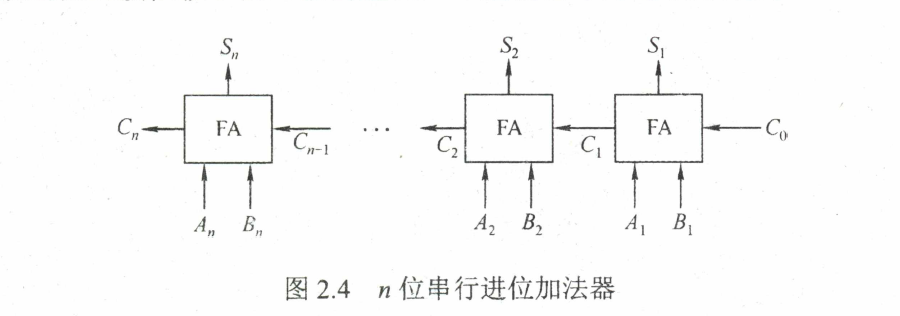
串行进位的并行加法器(行波进位加法器, Ripple-Carry Adders, RIP)

并行进位的并行加法器(超前进位加法器, Carry-Lookahead Adders, CLA)

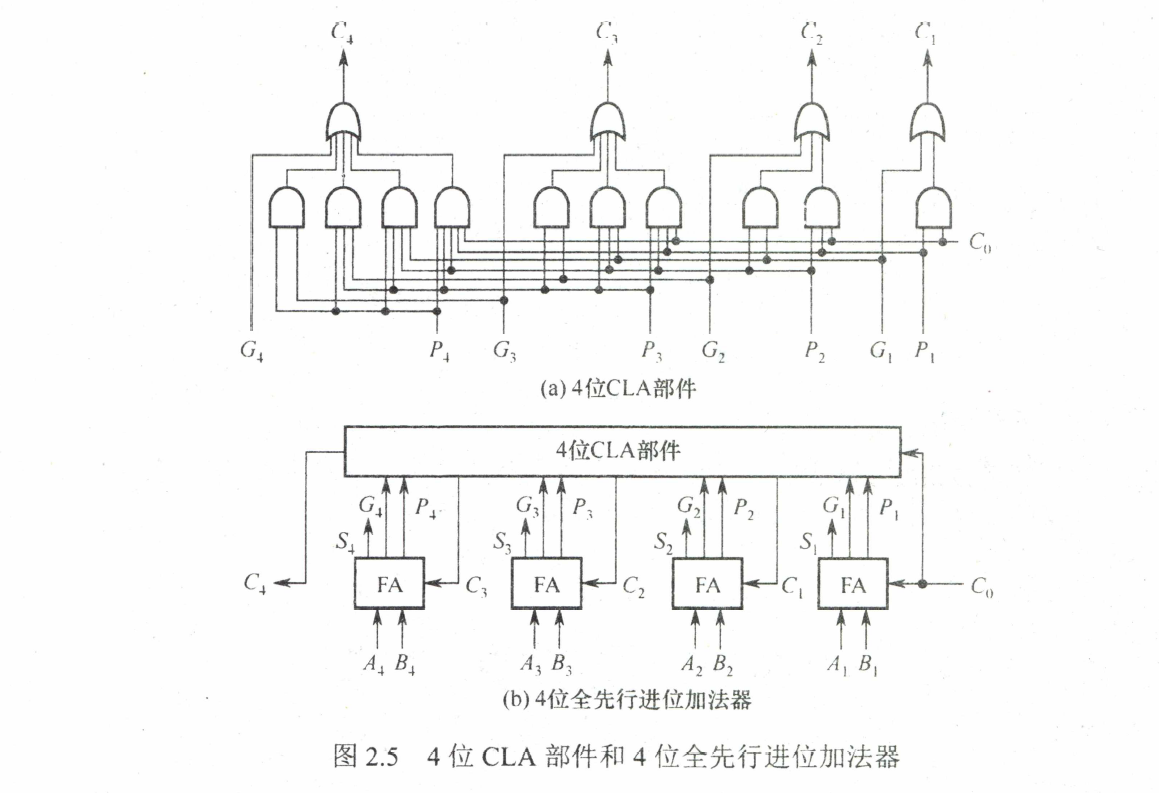
令 $ G_{i} = A_{i} B_{i}, P_{i} = A_{i} \oplus B_{i} $,全加器进位表达式为
$$
C_{i} = G_{i} + P_{i}C_{i - 1} (G_{i} = 1 或 P_{i}C_{i - 1} = 1 时, C_{i} = 1)
$$
当 $ A_{i} $ 与 $ B_{i} $ 都为1时, $ C_{i} = 1 $, 即有进位信号产生, 所以称 $ A_{i}B_{i} $ 为进位产生函数(本地进位), 用 $ G_{i} $ 表示。

当 $ A_{i} \oplus B_{i} = 1 $ 且 $ C_{i - 1} = 1 $ 时, $ C_{i} = 1 $ 。可视为 $ A_{i} \oplus B_{i} = 1 $, 第 $ i-1 $ 位的进位信号 $ C_{i - 1} $ 可以通过本位向高位传送。因此称 $ A_{i} \oplus B_{i}$ 为进位传递函数(进位传递条件), 用 $ P_{i} $ 表示。
$$
\begin{align}
C_{1} &= G_{1} + P_{1}C_{0} \\
C_{2} &= G_{2} + P_{2}C_{1} = G_{2} + P_{2}(G_{1} + P_{1}C_{0}) = G_{2} + P_{2}G_{1} + P_{2}P_{1}C_{0} \\
C_{3} &= G_{3} + P_{3}C_{2} = G_{3} + P_{3}(G_{2} + P_{2}G_{1} + P_{2}P_{1}C_{0}) = G_{3} + P_{3}G_{2} + P_{3}P_{2}G_{1} + P_{3}P_{2}P_{1}C_{0} \\
C_{4} &= G_{4} + P_{4}C_{3} = G_{4} + P_{4}(G_{3} + P_{3}G_{2} + P_{3}P_{2}G_{1} + P_{3}P_{2}P_{1}C_{0}) = G_{4} + P_{4}G_{3} + P_{4}P_{3}G_{2} + P_{4}P_{3}P_{2}G_{1} + P_{4}P_{3}P_{2}P_{1}C_{0}
\end{align}
$$

带标志的加法器

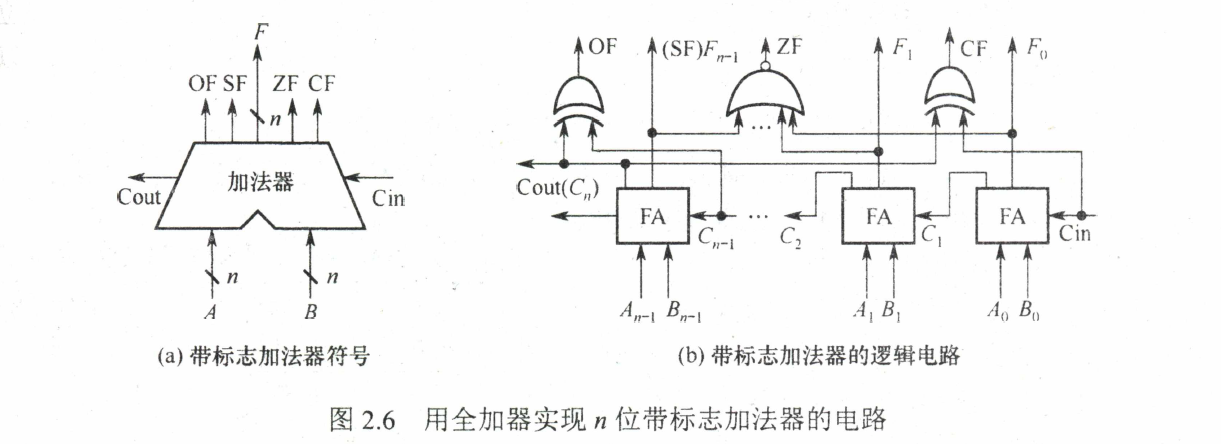
溢出标志(Overflow Flag, OF)

$$
OF = C_{n} \oplus C_{n - 1}
$$

符号标志(Sign Flag, SF)

$$
SF = S_{n}
$$

零标志(Zero Flag, ZF)

$$
ZF = S_{n} + S_{n - 1} + … + S_{2} + S_{1}
$$

进位/借位标志(Carry Flag, CF)

$$
CF = C_{out} \oplus C_{in} = C_{n} \oplus C_{0}
$$

定点数的移位运算

---

算数移位

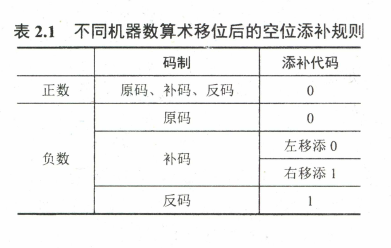
逻辑移位

循环移位

定点数的加减运算

---

原码的加减运算

补码的加减运算

负数补码, 最右边的1及其右边同原码, 最右边的1及其右边同反码。

$ [-A]_{补}: [A]_{补} $ 连同符号位一起取反加1。

补码加减运算电路

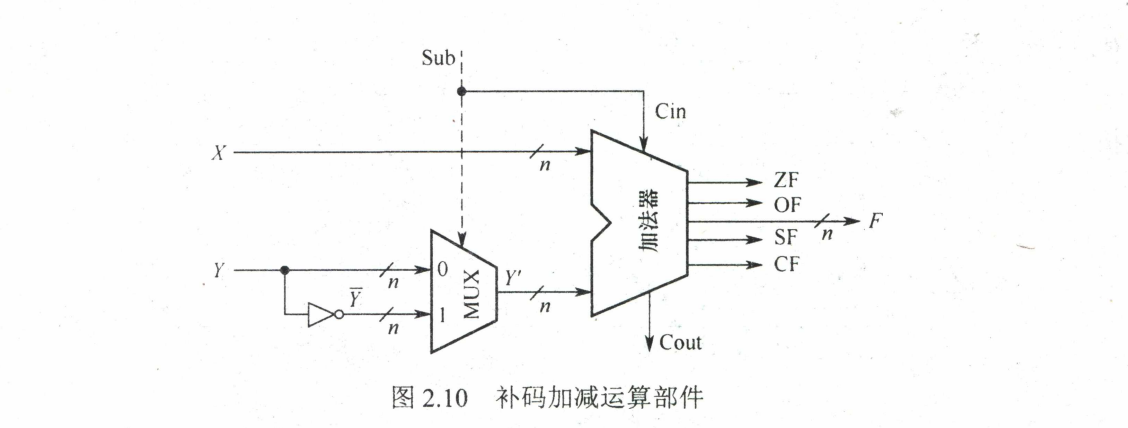
溢出判别方法

正数 + 正数 = 负数, 发生“上溢”。

负数 + 负数 = 正数, 发生“下溢”。

若 $ V $ = 0, 表示无溢出; 若 $ V $ = 1, 表示有溢出。

采用一位符号位

设A的符号为 $ A_{s} $, B的符号为$ B_{s} $, 运算结果的符号为 $ S_{s} $。

1. $ C_{s}C_{1} = 01 $: 发生正溢出。
2. $ C_{s}C_{1} = 10 $: 产生负溢出。

则溢出逻辑表达式为

$$
V = A_{s}B_{s} \bar{S_{s} } + \bar{A_{s} } \bar{B_{s} } S_{s}
$$
若 $ V $ = 0, 表示无溢出; 若 $ V $ = 1, 表示有溢出。

采用双符号位

单符号位法, 模2补码; 双符号位法, 模4补码。

运算结果的两个符号位 $ S_{1}S_{2} $ 相同, 表示未溢出;

运算结果的两个符号位 $ S_{1}S_{2} $ 不同, 表示溢出, 此时最高位符号位代表真正的符号。

符号位 $ S_{1}S_{2} $ 的各种情况如下:

1. $ S_{1}S_{2} $ = 00: 表示结果为正数, 无溢出。

2. $ S_{1}S_{2} $ = 01: 表示结果正溢出。

3. $ S_{1}S_{2} $ = 10: 表示结果负溢出。

4. $ S_{1}S_{2} $ = 11: 表示结果为负数, 无溢出。

溢出逻辑判断表达式为
$$
V = S_{1} \oplus S_{2}
$$

若 $ V $ = 0, 表示无溢出; 若 $ V $ = 1, 表示有溢出。

采用一号符号位根据数据位的进位情况判断溢出

若符号位的进位 $ C_{s} $ 与最高数位的进位 $ C_{1} $相同, 则说明没有溢出, 否则表示发生溢出。溢出逻辑判断表达式为:
$$
V= C_{s} \oplus C_{1}
$$

若 $ V $ = 0, 表示无溢出; 若 $ V $ = 1, 表示有溢出。

定点数的乘除运算

---

定点数的乘法运算

符号扩展

正数符号扩展，符号位不变，新表示形式的所有扩展位都用0进行填充。

负数符号扩展方法则根据机器数的不同而不同。

原码表示负数的符号扩展方法与正数相同，只不过此时符号位为1。

补码表示负数的符号扩展方法: 原有形式的符号位移动到新形式的符号位上，新表示形式的所有附加位都用1(对于整数)或0(对于小数)进行填充。

原码一位乘法

设 $ [X]_{原} = x_{s}.x_{1}x_{2}···x_{n}, [Y]_{原} = y_{s}.y_{1}y_{2}···y_{n} $

1. 被乘数和乘数均取绝对值参加运算, 看作无符号数, 符号位为 $ x_{s} \oplus y_{s} $ 。

2. 部分积是乘法过程的中间结果。乘数的每一位 $ y_{i} $ 乘以被乘数得 $ X \times y_{i} $ 后, 将该结果与前面所得的结果累加, 就是部分积, 初值为0。

3. 从乘数的最低位开始判断, 若 $ y_{n} $ = 1, 则部分积加上被乘数 $ |x| $, 然后右移一位; 若 $ y_{n} $ = 0, 则部分积加上0, 然后右移一位。

4. 重复步骤3, 判断n次。

运算器实现

符号位 = $ S_{X_{被乘数} } \oplus S_{X_{被乘数} } $

1. $ | X_{被乘数} | \to X $

2. $ | X_{乘数} | \to MQ $ (MQ存储乘数, 乘积低位)

3. $ 置零ACC $ (ACC存储乘积高位, 高位和低位称为部分积)

4. $ if[(MQ)_{0} = 1], (ACC) + (X) \to ACC $

   $if[(MQ)_{0} = 0], (ACC) + 0 \to ACC $

5. $ [(ACC + MQ) >> 1] \to (ACC + MQ) $ (逻辑右移)

6. 重复45, 直到MQ全是乘积低位, 没乘数位

7. $ 符号位 \to (ACC)n $

8. 结果是 (ACC + MQ)

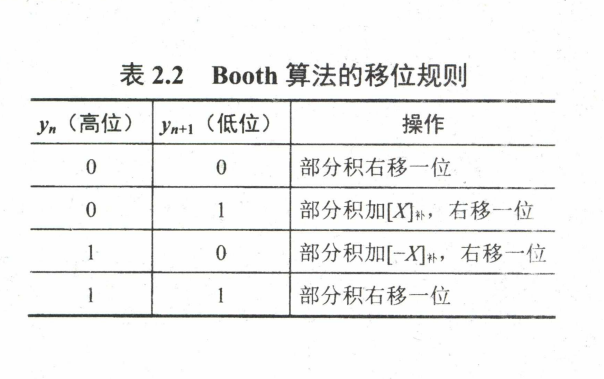
补码一位乘法(Booth算法)

设 $ [X]_{补} = x_{s}.x_{1}x_{2}···x_{n}, [Y]_{补} = y_{s}.y_{1}y_{2}···y_{n} $

1. 符号位参与运算, 运算的数均以补码表示。

2. 被乘数一般取双符号位参与运算, 部分积取双符号位, 初值为0, 乘数取单符号位。

3. 乘数末位增设附加位 $ y_{n + 1} $, 初值为0。

4. 根据($ y_{n}, y_{n + 1} $)的取值来确定操作。

5. 移位按补码右移规则进行。

6. 按照上述算法进行n+1步操作, 但第n+1步不再移位(共进行n+1次累加和n次右移),仅根据 $ {y_n} $ 与 $ y_{n + 1} $ 的比较结果做相应的运算。

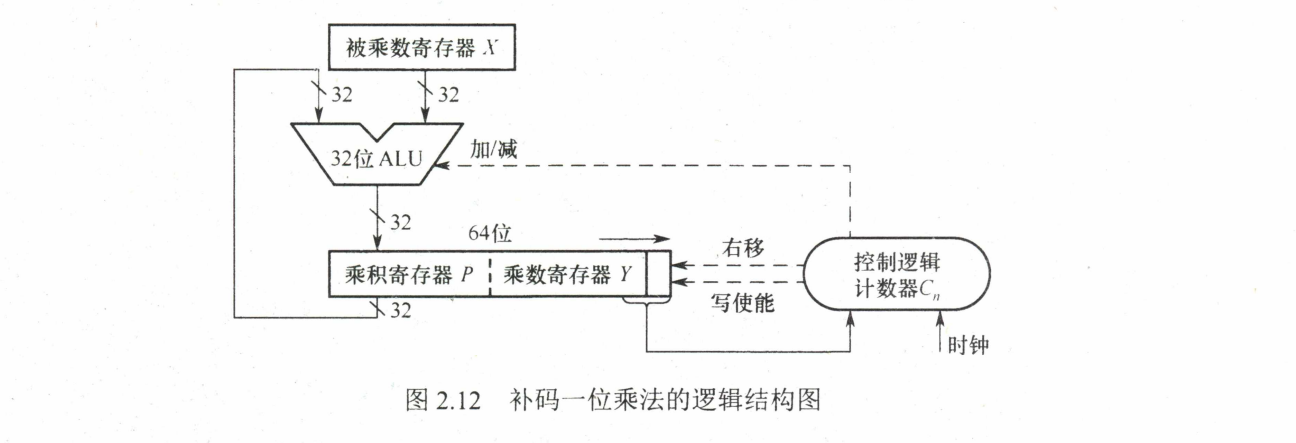
运算器实现

1. $ [X_{被乘数}]_{补(双符号位)} \to X $

2. $ [ X_{乘数} ]_{补(单符号位)} \to (MQ)_{1-n}, 0 \to (MQ)_{0} $ ($ MQ_{0} $ 称为辅助位)

3. $ 置零ACC $ (ACC也采用双符号位)

4. $ if[(MQ)_{0} - (MQ)_{1} = 1], (ACC) + (X) \to ACC $

$ if[(MQ)_{0} - (MQ)_{1} = 0], (ACC) + 0 \to ACC $

$ if[(MQ)_{0} - (MQ)_{1} = -1], (ACC) + [(-X)]_{补} \to ACC $ (有辅助电路, 把 $ [x]_{补} $ 快速转换成 $
[-x]_{补} $)

5. $ [(ACC + MQ) >> 1] \to (ACC + MQ) $ (算数右移)

6. 重复45, 直到MQ剩乘数原符号位, 执行一次4。

7. 结果是 (ACC + $ MQ_{n - 1} $) (ACC是双符号位)

补码乘法运算电路

定点数的除法运算

原码除法运算(相同步骤抽象)

设被除数 $ [X]_{原} = x_{s}.x_{1}x_{2}···x_{n} $, 除数 $ [Y]_{原} = y_{s}.y_{1}y_{2}···y_{n} $

1. 商的符号: $ Q_{s} = x_{s} \oplus y_{s} $。
2. 商的数值: $ |Q| = |X| / |Y| $。

(定点小数，规定$ |X| \gt |Y| $)

运算器实现

符号位 = $ S_{X_{被乘数} } \oplus S_{X_{被乘数} } $

1. $ | X_{被除数} | \to ACC $ (ACC存储被除数, 余数)

2. $ | X_{除数} | \to X $

3. $ 置零MQ $ (MQ低位为待确定的商)

(定点小数, 第一次执行, 商必须是0, 否则违反$ |X| \gt |Y| $)

原码除法运算(恢复余数法)

当余数为负时, 商上0，余数加回除数，左移一位。

运算器实现

1. $ 先上商1 \to MQ_{0}, (ACC) - (X) \to ACC $ $ \{(ACC) - (X) = (ACC) + [-(X)] = (ACC) + [-(X)]_{补} \} $
2. $ if[(ACC)_{n} = 1], (ACC) + (X) \to ACC, 0 \to MQ_{0} $ $ \{ (ACC) + (X) = (ACC) + [(X)]_{补}
   \} $
3. $ [(ACC + MQ) << 1] \to (ACC + MQ) $ (逻辑左移, 最后一次不用)
4. 重复123, 直到MQ全是商。
5. $ 符号位 \to (MQ)n $
6. 商是(MQ), 余数是(ACC)

(最后一位不够除，也要恢复)

原码除法运算(不恢复余数法, 加减交替法)

当余数为正时，商上1，余数和商左移一位，再减去除数;

当余数为负时，商上0，余数和商左移一位，再加上除数;

当第n+1步余数为负时，需加上Y得到第n+1步正确的余数(余数与被除数同号)。
$$
[a(负) + b] << 1 - b = 2a + b = a << 1 + b
$$

运算器实现

1. $ 1 \to MQ_{0}, (ACC) - (X) \to ACC $ $ \{(ACC) - (X) = (ACC) + [-(X)] = (ACC) + [-(X)]_{补} \} $(第一次不执行3)
2. $ if[(ACC)_{n} = 1], 0 \to MQ_{0}, 在3左移后, (ACC) + (X) \to ACC $
3. $ if[(ACC)_{n} = 0], 0 \to MQ_{0}, 在3左移后, (ACC) - (X) \to ACC $
4. $ [(ACC + MQ) << 1] \to (ACC + MQ) $ (逻辑左移, 最后一次不用)
5. 重复234, 直到MQ全是商。
6. $ 符号位 \to (MQ)n $
7. 商是(MQ), 余数是(ACC)

(最后一位不够除，也要恢复)

补码除法运算(加减交替法)

1. 符号位与数值位一起参加运算。
2. 根据被除数和除数的符号决定是做加法还是减法, 上商的原则根据余数和除数的符号位共同决定，同号上商“1”，异号上商“0”:最后一步商恒置“1”
3. 除数与被除数均用补码表示，商和余数也用补码表示, 都采用双符号位。
4. 若被除数与除数同号，则被除数减去除数; 若被除数与除数异号，则被除数加上除数。
5. 若余数与除数同号，则商上1，余数左移一位减去除数; 若余数与除数异号，则商上0, 余数左移一位加上除数。
6. 重复执行操作5。
7. 若对商的精度没有特殊要求，则一般采用“末位恒置1”法。

除法运算电路

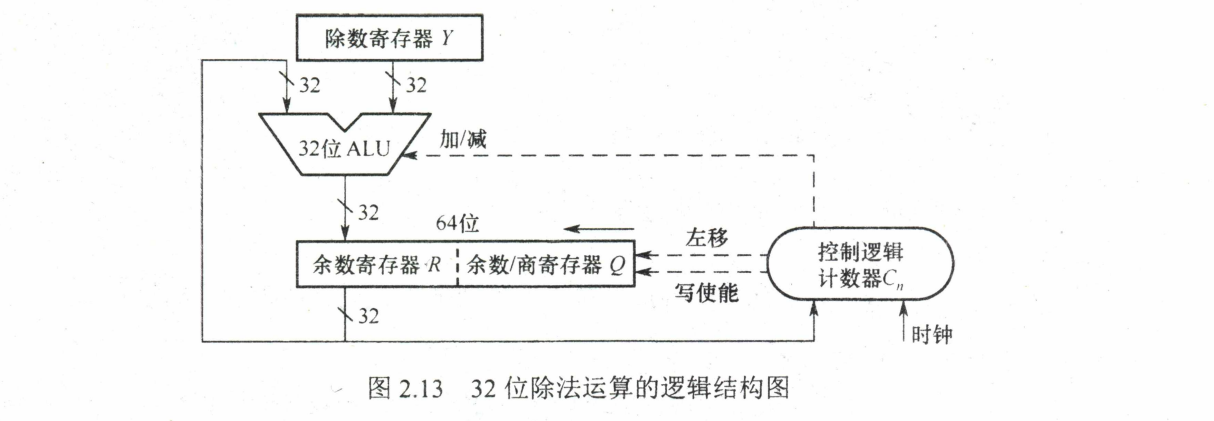
数据的存储和排列

---

数据的“大端方式”和“小端方式”存储

最高有效字节(Most Significant Byte, MSB)

最低有效字节(Least Significant Byte, LSB)

大端方式

大端方式按从最高有效字节到最低有效字节的顺序存储数据，即最高有效字节存放在前面，便于人类阅读。

小端方式

小端方式按从最低有效字节到最高有效字节的顺序存储数据，即最低有效字节存放在前面，便于机器处理。

数据按“边界对齐”方式存储

按字节编址，每个字节对应一个地址。

边界对齐方式

无论所取的数据是字节、半字还是字，均可一次访存取出。所存储的数据不满足上述要求时，通过填充空白字节使其符合要求。这样虽然浪费了一些存储空间，但可提高取指令和取数的速度。

边界不对齐方式

数据不按边界对齐方式存储时，可以充分利用存储空间，但半字长或字长的指令可能会存储在两个存储字中，此时需要两次访存，并且对高低字节的位置进行调整、连接之后才能得到所要的指令或数据，从而影响了指令的执行效率。

补充

---

ALU属于什么类型的电路

ALU是由组合逻辑电路构成的，最基本的部件是并行加法器。

由于单纯的ALU 不能够存储运算结果和中间变量，往往将ALU和寄存器或暂存器相连。

构成运算器的部件

ALU为运算器核心，数据总线供 ALU 与外界交互数据使用，溢出标志即为一个状态寄存器。

地址寄存器不属于运算器，而属于存储器, 区分在CPU中的地址寄存器。

补码加减运算电路

负数，输入取反，进位为1。

---

COPYRIGHT (c) OLENCER. ALL RIGHTS RESERVED.