浮点数的表示与运算

浮点数的表示

---

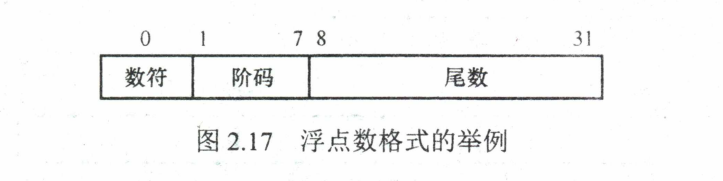
浮点数的表示格式

浮点数通常表示为:
$$
N = (-1)^{S} \times M \times R^{E}
$$
$ S $ 数符, 决定浮点数符号。

$ M $ 尾数, 二进制定点小数, 一般原码表示。

$ E $ 阶码, 二进制定点整数, 移码表示, 由阶符和阶码的数值部分组成。

$ R $ 基数, 可约定2、4、16等。

浮点数的表示范围

运算结果大于最大正数时称为正上溢，小于绝对值最大负数时称为负上溢，正上溢和负上溢统称上溢。

运算结果在0至最小正数之间时称为正下溢，在0至绝对值最小负数之间时称为负下溢，正下溢和负下溢统称下溢。

数据一旦产生上溢，计算机必须中断运算操作，进行溢出处理。

数据下溢时，浮点数值趋于零，计算机仅将其当作机器零处理。

浮点数的规格化

左规格化

当运算结果的尾数的最高数位不是有效位, 即出现 $ 0.0···01x···x $的形式时，进行左规。

左规时，尾数每左移一位、阶码减1(基数为 2时)。左规可能需要要进行多次。

右规格化

当运算结果的尾数的有效位进到小数点前面时，需要进行右规。

将尾数右移一位、阶码加1(基数为2时)。需要右规时，只需进行一次。

规格化尾数

$ \frac{1}{R} \leq | M | \lt 1 $

原码

正数, 0.1x···x, 最大值0.11···1, 最小值0.10···0, $ \frac{1}{2} \leq M \leq 1 - 2^{-n} $。

负数, 1.1x···x, 最大值1.10···0, 最小值1.11···1, $ -(1 - 2^{-n}) \leq M \leq -\frac{1}{2} $。

补码

正数, 0.1x···x, 最大值0.11···1, 最小值0.10···0, $ \frac{1}{2} \leq M \leq 1 - 2^{-n} $。

负数, 1.0x···x, 最大值1.01···1, 最小值1.00···0, $ -1 \leq M \leq -(\frac{1}{2} + 2^{-n}) $。

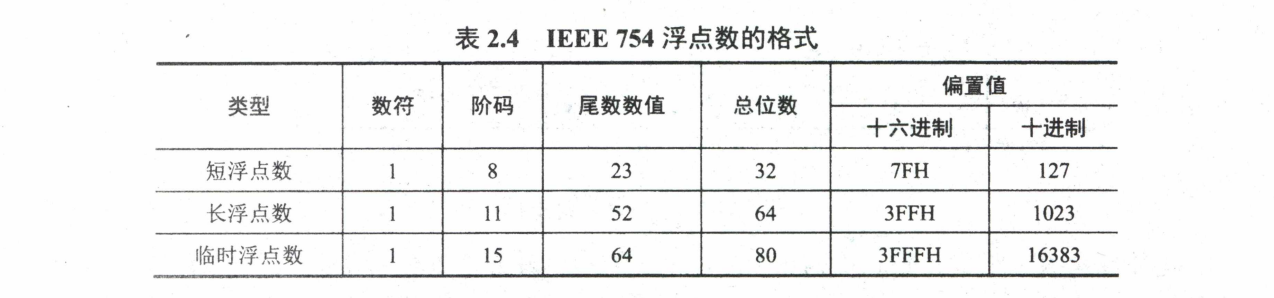
IEEE 754

基数 $ R $ 隐含为2, 尾数 $ M $ 用采取隐藏位策略的原码表示, 且阶码 $ E $ 用移码(偏置值为 $ 2^{n} - 1 $)表示的浮点数。

最小绝对值

$ (1.0)_{2} \times 2^{-126} $

最大绝对值

$ (1.1···1)_{2} \times 2^{127}$

阶码全0全1特殊用法

全0阶码全0尾数: $ \pm 0 $, 零的符号取决于数符 $ S $, 一般情况下 $ +0 $ 和 $ -0 $ 是等效的。

全0阶码不全0尾数: 非规格化小数, $ \pm (0.xx···x)2^{-126} $。

全1阶码全0尾数: $ \pm\infty $, $ +\infty $ 在数值上大于所有有限数, $ -\infty $ 则小于所有有限数。引入无穷大数的目的是，在计算过程出现异常的情况下使得程序能继续进行下去。

全1阶码不全0尾数: NaN。

定点、浮点表示的区别

数值的表示范围

若定点数和浮点数的字长相同，则浮点表示法所能表示的数值范围远大于定点表示法。

精度

对于字长相同的定点数和浮点数来说，浮点数虽然扩大了数的表示范围，但精度降低了。

数的运算

浮点数包括阶码和尾数两部分，运算时不仅要做尾数的运算，还要做阶码的运算，而且运算结果要求规格化，所以浮点运算比定点运算复杂。

溢出问题

在定点运算中，当运算结果超出数的表示范围时，发生溢出; 浮点运算中，运算结果超出尾数表示范围却不一定溢出，只有规格化后阶码超出所能表示的范围时，才发生溢出。

浮点数的加减运算

---

对阶

小阶向大阶看齐的原则。

小阶尾数右移, 加阶码, 影响精度。

尾数求和

规格化

需要左规, 左规可能需要多次; 需要右规, 右规只需一次。

舍入

在对阶和尾数右规时，可能会对尾数进行右移，为保证运算精度，一般将低位移出的两位保留下来，参加中间过程的运算，最后将运算结果进行舍入，还原表示成IEEE 754 格式。

舍1入法

运算结果保留位的最高数位为0，则舍去;最高数位为1，则在尾数的末位加1。

这样可能会使尾数溢出，此时需再做一次右规。

恒置1法

不论丢掉的最高数位是0还是1，都把右移后的尾数末位恒置1。

截断法 (恒舍法)。

直接截取所需位数，丢弃后面的所有位，这种舍入处理最简单。

溢出判断

右规和尾数舍入, 数值很大的尾数舍入时，可能因为末位加1而发生尾数溢出，此时需要通过右规来调整尾数和阶。

右规时阶加1，导致阶增大，因此需要判断是否发生了指数上溢。当调整前的阶码为11111110时，加1后，会变成 11111111而发生指数上溢。

左规。左规时阶减1，导致阶减小，因此需要判断是否发生了指数下溢。其判断规则与指数上溢类似，左规一次，阶码减 1，然后判断阶码是否为全0来确定是否指数下溢。

注某些题目可能会指定尾数或阶码采用补码表示。通常采用双符号位，当尾数求和结果溢出(如尾数为 10.xx···x 或 01.xx···x)时，需右规一次; 当结果出现 00.0xx···x或11.1xx···x时，需要左规，直到尾数变为 00.1xx···x或 11.0xx···x。

补充

---

采用规格化浮点数的目的

与非规格化浮点数相比，采用规格化浮点数的目的主要是为了增加数据的表示精度。

舍入

舍入是浮点数的概念，定点数没有舍入的概念。

浮点数舍入的情况有两种:对阶、右规格化。

---

COPYRIGHT (c) OLENCER. ALL RIGHTS RESERVED.